Directional Lights I
| Prev: Lighting | Next: Directional Lights II |
The equations in here are from the chapter “The Mathematics of Lighting” from the book “OpenGL Programming Guide”, aka the Red Book.
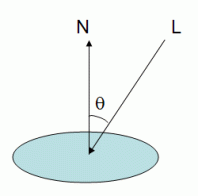
We’ll start with the diffuse term. The diffuse lighting in OpenGL assumes that the light is perceived with the same intensity regardless of the viewer’s position. Its intensity is proportional to both the lights diffuse intensity as well as material’s diffuse reflection coefficient. The intensity is also proportional to the angle between the light direction and the normal of the surface.
The following formula is used in OpenGL to compute the diffuse term:
where I is the reflected intensity, Ld is the light’s diffuse color (gl_LightSource[0].diffuse), and Md is the material’s diffuse coefficient (gl_FrontMaterial.diffuse).
This is known as Lambertian Reflection. ‘Lambert’s cosine law’ states that the apparent brightness of a diffusely radiating plane surface is proportional to the cosine of the angle formed by the incident’s light direction and the normal to the surface. This was more than 200 years ago (Johann Heinrich Lambert, 1728-1777)!
The vertex shader to implement this formula will use the lights properties, namely its position, and diffuse intensity. It will also use the materials diffuse setting. Hence to use this shader just set the light as usual in OpenGL. Note however that since we’re not using the fixed functionality, there is no need to enable the lights.
Since we need to compute a cosine, first we’re going to make sure that the normal vector and the light direction vector (gl_LightSource[0].position) are normalized, and then we’ll use the dot product to get the cosine. Note that, for directional lights, OpenGL stores the light direction as the vector from the vertex to the light source, which is the opposite to what is shown in the above figure.
OpenGL stores the lights direction in eye space coordinates; hence we need to transform the normal to eye space in order to compute the dot product. To transform the normal to eye space we will use the pre-defined uniform variable mat3 gl_NormalMatrix. This matrix is the transpose of the inverse of the 3×3 upper left sub matrix from the modelview matrix.
The following vertex shader shows the GLSL code to achieve this.
void main() {
vec3 normal, lightDir;
vec4 diffuse;
float NdotL;
/* first transform the normal into eye space and normalize the result */
normal = normalize(gl_NormalMatrix * gl_Normal);
/* now normalize the light's direction. Note that according to the
OpenGL specification, the light is stored in eye space. Also since
we're talking about a directional light, the position field is actually
direction */
lightDir = normalize(vec3(gl_LightSource[0].position));
/* compute the cos of the angle between the normal and lights direction.
The light is directional so the direction is constant for every vertex.
Since these two are normalized the cosine is the dot product. We also
need to clamp the result to the [0,1] range. */
NdotL = max(dot(normal, lightDir), 0.0);
/* Compute the diffuse term */
diffuse = gl_FrontMaterial.diffuse * gl_LightSource[0].diffuse;
gl_FrontColor = NdotL * diffuse;
gl_Position = ftransform();
}
Now in the fragment shader all there is left to do is setting the fragments color, using the varying gl_Color variable.
void main()
{
gl_FragColor = gl_Color;
}
The following image shows this shader applied to the teapot. Note that the bottom of the teapot is too dark. This is because we’re not taking into account the ambient lighting terms available in OpenGL.
 Incorporating the ambient terms is also easy to do. There is a global ambient term and a light ambient term. The formula for the ambient term is as follows:
Incorporating the ambient terms is also easy to do. There is a global ambient term and a light ambient term. The formula for the ambient term is as follows:
The vertex shader needs to add a few instructions to compute the ambient term:
void main()
{
vec3 normal, lightDir;
vec4 diffuse, ambient, globalAmbient;
float NdotL;
normal = normalize(gl_NormalMatrix * gl_Normal);
lightDir = normalize(vec3(gl_LightSource[0].position));
NdotL = max(dot(normal, lightDir), 0.0);
diffuse = gl_FrontMaterial.diffuse * gl_LightSource[0].diffuse;
/* Compute the ambient and globalAmbient terms */
ambient = gl_FrontMaterial.ambient * gl_LightSource[0].ambient;
globalAmbient = gl_LightModel.ambient * gl_FrontMaterial.ambient;
gl_FrontColor = NdotL * diffuse + globalAmbient + ambient;
gl_Position = ftransform();
}
The following image shows the end result. Adding an ambient term washes out color, but it’s a cheap workaround for the lack of a global illumination model where light bounces, and hence it affects surfaces not directly affected by the light source.
Move on to the next section for the specular component.
| Prev: Lighting | Next: Directional Lights II |
4 Responses to “Directional Lights I”
Leave a Reply to RiverC Cancel reply
This site uses Akismet to reduce spam. Learn how your comment data is processed.


Here’s a question I’m struggling with on GL_LIGHT, particularly on these directional lights.
The default directional light position is
(0,0,1,0)
what direction is this light supposed to be coming from? Behind the camera?
What would one do to get different directions? For my part, only manipulating Z changes anything, but all it does is turn off the light if I set it to 0: (0,0,0,0).
Let’s say I’d like to produce a directional light from above (like the passive light produced by the sky at all times) what would I need to set the Position values to, and why?
When I read this article I feel a contradiction: first it is said that the diffusion intensity does not depend on the viewers position, but Lambert’s cosine law states that … is proportional to the cosine of the angle formed by the line of sight and …
Well spotted. I meant the light’s direction, not the line of sight 🙂
Fixed.
Don’t you miss a “-” at this line ?
lightDir = normalize(vec3(gl_LightSource[0].position));
I would write :
lightDir = normalize(vec3(- gl_LightSource[0].position));
Because you said :
OpenGL stores the light direction as the vector from the vertex to the light source, which is the opposite to what is shown in the above figure