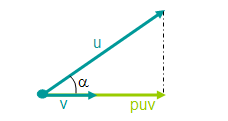
Consider two vectors v and u. The purpose of this section is to show how to compute the projection of vector u onto vector v.
The vector puv is the projection of vector u on vector v.
As v and puv share the same direction, and assuming the v is normalized, puv can be defined as:
where |puv| stands for the length of puv. So finding out |puv| allows us to easily find vector puv. The relation between the length of u and puv is given by the cosine of the angle between them.
The definition of the dot product says that
Hence, the value of the length of vector puv is:
So, looking back at the first equation, vector puv is defined as:
If vector v is normalized, i.e. it has unit length, then the division can be spared.
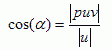
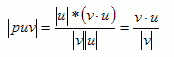
Note that this final formula for puv already assumes that v is normalized. If v is not normalized, then you have to divide by the square of |v|, instead of just |v|. So, if v is not normalized, you need to use the formula:
puv = ( Dot(v,u) / (|v|^2) ) * v
send me worked examples