


|
Billboarding Tutorial Index Cheating - Fast and Easy Cheating - Faster but not so Easy True Billboards |
| [Previous: Cheating Faster] | [Next: Spherical] |
Billboarding Tutorial
Cylindrical Billboards
True cylindrical billboarding constraints the objects rotation to an axis, as in the cheating version, but the look at vector from the object will be rotated in the camera's direction, restricted to the plane defined by the up vector, and the center of the local origin. The following image shows what happens.
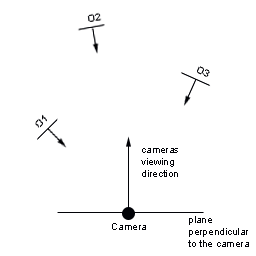
The method presented in here requires that you know where the object is in world coordinates, as well as the targets position, also in world coordinates. Usually the target is the camera's position which known. However the same may not be true for the object. If the object is positioned in the world through geometric transformations, such as translations and rotations, then keeping track of its position in world coordinates can be a hard task. We'll come back to this issue in a later section.
Assuming that both the objects and target positions are known in world coordinates, then billboarding becomes a simple geometrical operation.
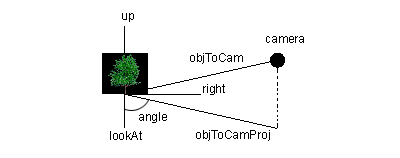
For simplicity reasons it is assumed that the object has the following vectors:
In order to orientate the object a rotation is performed around the up vector, by the angle between the lookAt vector and the vector from the object to the camera.
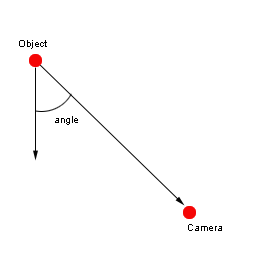
If objToCamProj is normalized then the inner product between lookAt and objToCam will allow the computation of the cosine of the angle. However knowing the cosine alone is not enough, since the cos(a) = cos(-a). Computing the cross product as well allows us to uniquely determine the angle. The cross product vector will have the same direction as the up vector if the angle is positive. For negative angles the up vector's direction will opposed to the up vector, effectively reversing the rotation.
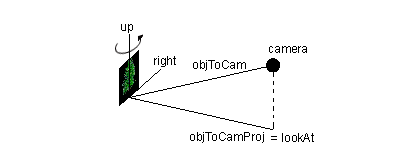
void billboardCylindricalBegin(
float camX, float camY, float camZ,
float objPosX, float objPosY, float objPosZ) {
float lookAt[3],objToCamProj[3],upAux[3];
float modelview[16],angleCosine;
glPushMatrix();
// objToCamProj is the vector in world coordinates from the
// local origin to the camera projected in the XZ plane
objToCamProj[0] = camX - objPosX ;
objToCamProj[1] = 0;
objToCamProj[2] = camZ - objPosZ ;
// This is the original lookAt vector for the object
// in world coordinates
lookAt[0] = 0;
lookAt[1] = 0;
lookAt[2] = 1;
// normalize both vectors to get the cosine directly afterwards
mathsNormalize(objToCamProj);
// easy fix to determine wether the angle is negative or positive
// for positive angles upAux will be a vector pointing in the
// positive y direction, otherwise upAux will point downwards
// effectively reversing the rotation.
mathsCrossProduct(upAux,lookAt,objToCamProj);
// compute the angle
angleCosine = mathsInnerProduct(lookAt,objToCamProj);
// perform the rotation. The if statement is used for stability reasons
// if the lookAt and objToCamProj vectors are too close together then
// |angleCosine| could be bigger than 1 due to lack of precision
if ((angleCosine < 0.99990) && (angleCosine > -0.9999))
glRotatef(acos(angleCosine)*180/3.14,upAux[0], upAux[1], upAux[2]);
}
The function billboardEnd() should be called after rendering the object as shown in the following example.
billboardCylindricalBegin(cx,cy,cz,ox,oy,oz);
drawObject();
billboardEnd();
| [Previous: Cheating Faster] | [Next: Spherical] |