Billboarding Tutorial

Cheating - Faster but not so easy

As mentioned before to get a cheating version of a billboard it is enough to reverse the orientations of the top 3x3 submatrix from the modelview matrix. The previous sections achieved this by setting this submatrix such that the appropriate transformations were reversed.

In here an alternative approach is presented. This is also a popular approach, it even got mentioned in the book OpenGL Game Programming.

Instead of changing the modelview matrix, the vertices of the billboard are manually transformed. This transformation effectively reverses the orientations present in the modelview matrix. The end result is the same as the one presented in the previous sections.

The vertices of the billboard are defined using up and right vectors that reverse the orientations of the modelview matrix. These vectors can be extracted from the inverse of M1.

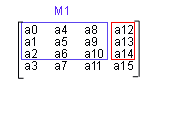
Fortunately, for an orthogonal matrix, the inverse is equal to the transpose. Is M1 orthogonal? It should be. If you're only using gluLookAt to perform you're camera movements, or just doing translations and rotations to the camera, then M1 is orthogonal. If, on the other hand you mess around with the modelview matrix then you may end up with M1 not being orthogonal.

Just in case you're wondering what the $%*# is a transpose, a matrix A is a tranpose of B, AT = B, if aij = bji, for every element.

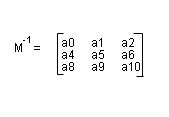
So what is an orthogonal matrix? As mentioned before, a square matrix Q is orthogonal if Q x QT = I, where QT is the transpose of Q and I is the identity matrix. In practice this means that the multiplying any two different columns or rows returns zero. This means that the dot product is zero, and therefore that the vectors are at right angles. It also means that multiplying a vector by itself should give 1, i.e. the vectors are normalized. So now that you know you can write your own routine to see if a matrix is orthogonal.

So we can easily get the inverse of M1. The first column of the inverse of M1 is the required right vector, and the second column represents the up required vector.

    
right = [a0,a4,a8]
up =	[a1,a5,a9]

Two examples of a quad billboard are now presented to show how to define the vertices. Assume that the quads edges have a length size.

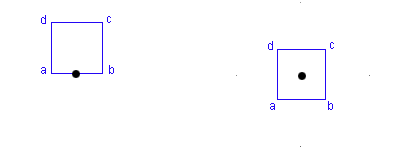
First a quad with the center at the bottom origin is presented (left figure).

    
a = center - right * (size * 0.5);
b = center + right * size * 0.5;
c = center + right * size * 0.5 + up * size;
d = center - right * size * 0.5 + up * size;

The right figure represents a quad with a centre on the middle of the quad. Its vertices are defined as:

    
a = center - (right + up) * size;
b = center + (right - up) * size;
c = center + (right + up) * size;
d = center - (right - up) * size;

When compared to the previous method you only get the modelview matrix once per frame. On the other hand you have to manually transform the vertices of the billboard. Overall this method is faster for quads, only 4 vertices, but harder to implement. If however you try to billboard an object with a larger number of vertices then the previous method could perform better.

In the source code a function is provided to extract the up and right vectors

void l3dBillboardGetUpRightVector(float *up, float *right);

Parameters:

up - an array of 3 floats. The function sets this to be the up vector

right - an array of 3 floats. The function sets this to be the right vector

The source code is as follows:

    
void l3dBillboardGetUpRightVector(float *up,float *right) {

	float modelview[16];

	glGetFloatv(GL_MODELVIEW_MATRIX, modelview);

	right[0] = modelview[0];
	right[1] = modelview[4];
	right[2] = modelview[8];

	up[0] = modelview[1];
	up[1] = modelview[5];
	up[2] = modelview[9];
}

If what you're after is the cylindrical version of this method then just set the up vector to [0,1,0]. You can use the function l3dBillboardGetRightVector, provided in the source code, to get the right vector.

[Previous: Cheating Cylindrical] [Next: Cylindrical]