Terrain Tutorial

The Circles Algorithm

This algorithm is similar to the fault algorithm in the sense that some points are displaced upwards. The main differences reside in the way how the points are select and how the points are displaced. In the fault algorithm a line divided the terrain in two parts, points in one part where displaced upwards, whereas points in the other part where displaced downwards. In here a circle with a random center, and a user defined radius is computed. Points inside the circle are displaced upwards, whereas the remaining points will keep their height.

The points inside the circle are displaced according to a cosine function as shown in the next figure

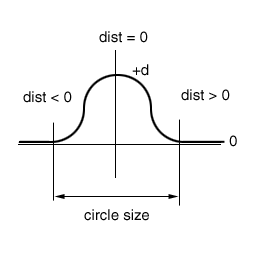
The next image shows a single iteration.

As you can see the algorithm is very simple. The first step is to find a random point which will be the center of the circle. Afterwards the points inside the circle are displaced using the following pseudocode.

    
for each terrain point (tx,tz) do

	pd = distance from circle center * 2 / terrainCircleSize
	
	if fabs(pd) <= 1.0
		
		height(tx,tz) +=  disp/2 + cos(pd*3.14)*disp/2;

where terrainCircleSize defines the circle size and disp defines the maximum height variation. As in the fault algorithm, the value of disp can be decreased as the number of iterations increases.

As usual there are endless variations to this algorithm, for instance try replacing the cosine with other functions. As an example, in the implementation provided, for each circle the height can be decreased or increased according to a random value, i.e. some iterations increase the height of the points inside the circle, whereas others will produce the symmetrical effect.

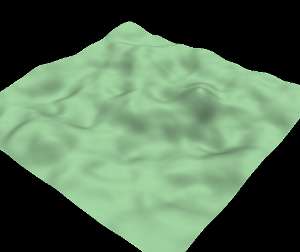
The following image is a screen shot of a terrain rendered with this algorithm after 1000 iterations.

[Previous: Simple Variations] [Next: Mid Point Displacement]